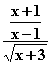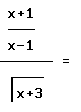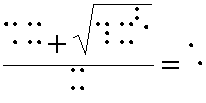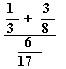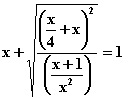Flavio Fogarolo - Centro di Documentazione e Formazione del Provveditorato agli Studi di Vicenza

"Software per la matematica con periferiche braille"

I problemi che sorgono quando si cerca di eseguire delle esercitazioni matematiche scolastiche con il computer e le periferiche braille sono molti, e per lo più di non facile soluzione.
L'uso di un software efficiente può essere d'aiuto, ma per affrontare seriamente il problema occorre considerare perlomeno altri due aspetti strettamente connessi: il codice e la simbologia.
Con il codice si considerano i metodi che vengono impiegati per trasformare un testo matematico scritto o stampato normalmente, con la sua ricchezza di forme e la sua organizzazione spaziale variamente articolata e connessa, in una sequenza di caratteri di contenuto equivalente ma ristrutturata in modo da essere accessibile attraverso la lettura tattile,
Con la simbologia si considerano invece i codici braille che possono essere impiegati per rappresentare i diversi simboli matematici.
Mentre per il braille tradizionale a 6 punti, ovvero quello scritto su carta, si è raggiunto, almeno a livello nazionale, una soddisfacente uniformità, per la scrittura al computer la situazione è ancora molto disomogenea.
Un sistema unico, ben condiviso, assolutamente non esiste e, probabilmente, non esisterà ancora per un pezzo. In effetti la presenza di vari metodi non è causata solo da un insufficiente coordinamento, ma da approcci diversi, basati anche su diversi presupposti e differenti bisogni degli utenti.
Ben diverse, ad esempio, sono sia le esigenze che le modalità d'uso di chi ha perso la vista da adulto e, conoscendo poco il braille, preferisce di gran lunga usare la sintesi vocale e si serve del linguaggio matematico al computer soprattutto per insegnare o scambiare ricerche, rispetto a quelle di un ragazzo in età scolare, abituato ad usare il braille come metodo quasi esclusivo di lettura, che deve imparare ad usare il linguaggio matematico man mano che si inoltra nella disciplina stessa e che lo usa prevalentemente, se non esclusivamente, per affrontare esercitazioni di calcolo.
Molti dei sistemi elaborarti finora, in varie parti del mondo, per la scrittura matematica dei non vedenti sono dei tipici prodotti del primo tipo, nati in ambiente universitario per le esigenze di comunicazione di utenti adulti e comunque già esperti nel calcolo: per questi motivi essi non possono essere impiegati proficuamente, così come sono, anche per i ragazzi delle nostre scuole.

Il software ideale, come vedremo, non esiste ancora. Potremo però cercare di definirne alcune caratteristiche.
Deve innanzitutto sviluppare al massimo i vantaggi che, nella pratica scolastica quotidiana, l'uso del computer può comportare, rispetto agli strumenti tradizionali, anche nella matematica.
Il principale è dato probabilmente dalla possibilità di leggere e scrivere, contemporaneamente, il testo matematico per analizzarlo ed operare le necessarie trasformazioni. Tra gli strumenti braille tradizionali solo la dattiloritmica consente di leggere e scrivere allo stesso tempo ma, come si sa, il suo uso è limitato a brevi operazioni.
Nella scuola italiana, dove la grande maggioranza dei ragazzi ciechi studiano in scuole comuni ed hanno quindi insegnanti di matematica che non conoscono la notazione braille, viene particolarmente apprezzata la possibilità di seguire sul video il lavoro dell’alunno ed intervenire quindi direttamente nell’azione didattica.
Infine il computer, che, essendo programmabile, è molto più potente di una normale macchina da scrivere, può fornire strumenti compensativi di analisi e supporto che, senza snaturare il compito con automatismi impropri, possono concorrere a superare parecchie delle più comuni difficoltà di gestione. Probabilmente molti di questi strumenti non sono stati ancora pensati (non dico progettati) ma già ora si possono vedere in atto alcune intuizioni brillanti, alcuni impieghi innovativi che, anche se non si può dire ancora fino a che punto siano utilizzabili in altri contesti, forniscono senza dubbio degli spunti interessanti e stimolanti.

Il metodo di Cristian Bernareggi
Decisamente innovativo è, ad esempio, il metodo usato dal Cristian Bernareggi, uno studente universitario di Milano che ha messo a punto, ai tempi del liceo, un sistema di scrittura matematica al computer su più livelli, molto simile a quello normale in nero.
Ad esempio, l'espressione (fig. 1)

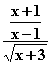
viene trascritta semplicemente (ricordiamoci che siamo in ambiente DOS) Fig.2:

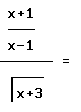
Scrive Cristian: "Nel leggere sulla barra braille un'espressione scritta in questo modo parto dal livello in cui compare l'uguale e poi mi muovo prima sopra e poi sotto se ho incontrato una linea di frazione oppure avanti verso destra se ho incontrato un'espressione. Se nel leggere un'espressione incontro un segno | (asci 179), mi sposto sopra per vedere se si tratta di una radice e se così controllo quale espressione si trova sotto la radice."
Cristian usa i simboli ASCII secondo la funzione che hanno a video: ^=esponente, ¥ =infinito, \/=disgiunzione logica, /\=congiunzione logica, p =pi greco, |x| =modulo… Come software usa un editor commerciale molto semplice al quale ha aggiunto delle macro che facilitano l'inserimento di simboli particolari non presenti in tastiera.
Sarebbe interessante capire fino a che punto l'uso di questo metodo, supportato magari da un editor di gestione più potente, potrebbe essere esteso e generalizzato. Fino a che punto, cioè, risulti più comodo ricostruire mentalmente un'equazione scritta in verticale rispetto alla disposizione in sequenza orizzontale, tradizionale del braille.

Dot Plus
Anche se nettamente diverso per finalità e modo di impiego, il metodo di Cristian Bernareggi ha qualche analogia con Dot Plus: entrambi, infatti, superano il vincolo della scrittura braille, tutta rigorosamente sequenziale, su di un'unica riga, per scegliere un'organizzazione spaziale a due dimensioni molto simile alla scrittura in nero.
Dot Plus, realizzato da un’équipe dell’Università dell’Oregon coordinata dal prof. Gardner, non è in realtà un programma, ma un insieme di font per Windows con alcune macro per Microsoft Word (quest'ultime, peraltro, poco funzionali).
Consente di preparare delle pagine matematiche da stampare in nero e trasformare poi a rilievo usando carta chimica e fornetto: è un sistema, quindi, di sola lettura, non interattivo, che può essere però molto più efficace del braille tradizionale soprattutto per testi di matematica superiore (studi di funzione, dimostrazione di teoremi) nei quali può inoltre essere utile l'inserimento di grafici.

Il testo matematico si scrive in modo normale (fig. 3):

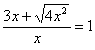
Poi si cambiano sia dimensioni che font: i numeri e i caratteri alfabetici si trasformano in braille, mentre operatori e segni di relazione rimango uguali. Per la loro forma stilizzata e le loro dimensioni essi saranno infatti leggibili anche al tatto (fig. 4).

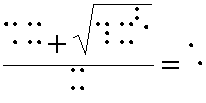
L'edizione americana usa un codice braille a 8 punti abbastanza simile a quello italiano, almeno nella rappresentazione dei numeri, ma con diverse incongruenze per cui sarebbe necessario, per un uso sistematico in Italia, per buona parte riscrivere il font (cosa, del resto, non complicatissima). Va detto però che l'interpretazione di simboli braille isolati, ovvero non inseriti in una riga, presenta varie difficoltà di interpretazione; è praticamente impossibile, ad esempio, distinguere una lettera f (punti 124) da un segno di addizione (punti 235) se non sono seguiti o preceduti da altri caratteri braille. Dot Plus risolve il problema aggiungendo ai caratteri di interpretazione dubbia un trattino orizzontale che indica il livello dei punti superiori (1 e 4).
Il sistema di Cristian Bernareggi e Dot Plus rappresentano, pur in modo diverso, due metodi decisamente innovativi per scrivere matematica con il computer. E, per quel che ho potuto vedere, praticamente unici nell'organizzazione in verticale delle formule.
Tutti gli altri metodi di scrittura matematica al computer preferiscono infatti il sistema orizzontale, con l'espressione trasferita su di un unica riga.
AMS, GS code e Triangle
Le soluzioni adottate sono però assai diverse per quanto riguarda i simboli utilizzati, soprattutto il modo in cui vengono attinti dalla dotazione standard dei codici ASCII del computer.
I due codici più completi attualmente in circolazione, l'AMS tedesco e il GS americano, fanno a questo proposito due scelte diametralmente opposte.
L'AMS usa solo i codici della serie principale, ossia quelli presenti sulla tastiera (a parte le vocali accentate) e pochi altri. Il vantaggio è dato da una maggiore uniformità di codici sulle periferiche braille (uniformità sempre relativa, perché anche in questo ambito le anomalie non mancano) e dal fatto che anche le sintesi pronunciano questi caratteri in modo abbastanza regolare.
I codici della serie principale liberamente utilizzabili sono però molto pochi (essa comprende infatti anche decine di caratteri dalla funzione immodificabile, come le lettere dell'alfabeto e i numeri) e quindi per rappresentare l'estrema varietà di simboli matematici è necessario ricorrere a combinazioni multiple, anche assai articolate.
Il codice braille usato negli USA è l'unico che fornisce una rappresentazione biunivoca e distinta tra tutti e 256 i codici ASCII e le 256 combinazioni possibili (2⁸) del codice a 8 punti . Il codice GS (Gardner-Salinas, ovvero i nomi dei due autori) sfrutta appieno questa potenzialità utilizzando un gran numero di codici particolari, tutti appartenenti alla serie ASCII estesa, da associare ai diversi simboli matematici in nero. Al codice GS è collegato il programma Triangle (realizzato dallo stesso team, che è, del resto, lo stesso che ha progettato anche Dot Plus), ovvero un editor matematico che facilita l'immissione dei codici speciali attraverso dei menù a scansione e dei pulsanti di scelta rapida, e cambia l'aspetto dei caratteri sul video assegnando loro delle forme che indicano in modo più evidente la funzione associata.

Ad esempio, un'espressione frazionaria di questo tipo (fig. 5):

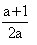
apparirà sul video in questo modo (notare i tre nuovi simboli aggiunti, non necessari nella versione originaria, che indicano l'inizio della frazione, la barra di frazione e la fine della frazione stessa) (fig. 6):

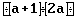
Triangle è inoltre fornito di una serie di programmi di adattamento per le sintesi vocali più diffuse in USA, che fanno in modo che i simboli speciali usati vengano pronunciati correttamente in base alla nuova funzione assunta, anziché al loro significato originario (ovviamente in inglese).
Per i limiti particolari derivanti dal codice (in particolare l'uso del braille americano) e per l'impostazione didattica legata chiaramente alla matematica superiore, Triangle non può (così com'è) essere di grande utilità per lo studente delle nostre scuole, ma può fornire senza dubbio diverse indicazioni utili per questo tipo di discussione. Alcune intuizioni, in particolare, appaiono preziose:

• l'uso di codici non standard, aumentando la gamma di simboli disponibili, migliora le potenzialità della rappresentazione tattile;
• è utile, se non indispensabile, predisporre dei sistemi amichevoli di immissione dei simboli non presenti in tastiera, (attraverso menù a scansione o combinazione di tasti);
• i codici ASCII utilizzati in modo non standard devono essere rappresentati a video in modo diverso, per facilitarne la lettura anche dai parte dei vedenti.

A onor del vero, Triangle offre anche altre utilità, soprattutto per lo studio delle funzioni e l'analisi dei relativi grafici, che però, in questo contesto ci interessano meno.

Il programma Erica e la matematica
L'approccio del programma Erica è un po' particolare; esso è stato progettato per fornire un ambiente di lavoro scolastico particolarmente amichevole, soprattutto per i bambini più piccoli delle elementari.
Progressivamente è stato adattato e potenziato in modo da poter rispondere anche alle esigenze degli studenti più grandi, soprattutto per quanto riguarda la matematica, ma la caratteristica originale di amichevolezza e attenzione alle esigenze dell'utente è rimasta ben presente e dominante. In generale si può dire che con Erica è il computer che si deve adattare ai bisogni e alle caratteristiche dell'alunno, e non viceversa.
Erica fornisce diverse funzioni utili per la gestione di testi matematici, sviluppate e potenziate anno dopo anno in base all'esperienza e all'uso reale del programma da parte di alcuni studenti. Ci si è concentrati in particolare sulle esercitazioni che prevedono la risoluzione di espressioni o equazioni attraverso successive modificazioni.
Anche se sviluppata autonomamente, la strategia adottata ha, come si può vedere, diverse analogie l'editor di Triangle.
Le caratteristiche principali della strategia utilizzata da Erica per la matematica sono:

1. uso quasi esclusivo del tastierino numerico di destra per la digitazione, oltre che dei numeri e dei principali operatori, anche di tutti gli altri simboli necessari, eventualmente combinati con Alt, Ctrl e Maiuscolo, in modo che l'immissione dei dati possa essere effettuata con la sola mano destra mentre la sinistra può controllare la riga mentre si scrive (questo significa poter leggere e scrivere contemporaneamente anche con la riga braille);
2. esecuzione dei calcoli parziali sulle varie righe con il metodo della correzione (in modalità sovrascrittura) del testo precedente;
3. funzione automatica per copiare sotto all'espressione l'ultima riga e compattarla eliminando gli spazi vuoti;
4. finestra di editor con margine destro lungo, in modo che nessuna riga dell'espressione venga spezzata andando a capo;
5. la riga viene copiata due volte affinché sopra a quella che viene modificata ne rimanga una di campione che (poiché non si va mai a capo) sarà sempre in corrispondenza verticale con quella che viene elaborata;
6. tutti i caratteri speciali avranno una rappresentazione braille sulla riga il più possibile coerente con quella del codice standard a sei punti e un disegno sul video che ricorda facilmente la funzione assegnata.
7. si usano dei caratteri speciali anche per i numeratori delle frazioni: sulla riga appariranno abbassati rispetto ai numeri corrispondenti, sul video sottolineati (questa tecnica vale solo per le frazioni tutte numeriche: se i termini sono letterali è inevitabile usare i delimitatori di frazione complessa);
8. programma interno di trascodifica sia per la stampa in braille che per quella in nero (in modo da rendere comunque leggibile il testo matematico, anche se si sono usati simboli non standard).
9. utilità che, attraverso la contrazione delle formule a più livelli, consente di cogliere rapidamente la struttura globale dell'espressione.

Qualche esempio. Uno sul metodo di trascrizione.

L'espressione (fig. 7):

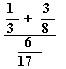
apparirà, con Erica, sul video in questo modo (fig. 8)

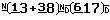
mentre e sulla riga braille si leggerà così (fig. 9):

Per confronto, con il codice AMS sarebbe apparsa sul video in questo modo:

((1/3)+(3/8))/(6/17)

e così con il GS (fig. 10):

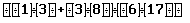
Ecco, invece, un esempio del metodo di risoluzione, per copiatura e correzione riga per riga:

partendo da questa espressione;

21•5÷[(5•4+56÷8)÷9+(63÷9+5-2)÷5]-20

con un semplice comando viene ricopiata:

21•5÷[(5•4+56÷8)÷9+(63÷9+5-2)÷5]-20

21•5÷[(5•4+56÷8)÷9+(63÷9+5-2)÷5]-20

quindi si effettuano i calcoli possibili sulla seconda riga; in caso di dubbio basta spostare il cursore in alto per poter consultare sempre, con esatta corrispondenza, la posizione di partenza.

21•5÷[(5•4+56÷8)÷9+(63÷9+5-2)÷5]-20

21•5÷[(20 + 7 )÷9+( 7 + 3 )÷5]-20

a questo punto, con il solito comando, l'ultima riga viene compattata (eliminando gli spazi vuoti e copiata due volte. Il cursore di posizione all'inizio dell'ultima riga.

21•5÷[(5•4+56÷8)÷9+(63÷9+5-2)÷5]-20

21•5÷[(20 + 7 )÷9+( 7 + 3 )÷5]-20

21•5÷[(20+7)÷9+(7+3)÷5]-20

21•5÷[(20+7)÷9+(7+3)÷5]-20

Si prosegue nello stesso modo finché tutta l'espressione è risolta. Alla fine apparirà così:

21•5÷[(5•4+56÷8)÷9+(63÷9+5-2)÷5]-20

21•5÷[(20 + 7 )÷9+( 7 + 3 )÷5]-20

21•5÷[(20+7)÷9+(7+3)÷5]-20

21•5÷[ 27 ÷9+ 10 ÷5]-20

21•5÷[27÷9+10÷5]-20

21•5÷[ 3 + 2 ]-20

21•5÷[3+2]-20

21•5÷ 5 -20

21•5÷5-20

21-20=1

Infine un esempio sull'utilità di contrazione per facilitare la comprensione della struttura globale del testo matematico.

L'espressione (fig. 11)

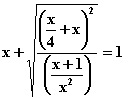
verrà trasformata in Erica in questo modo (fig. 12):

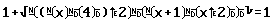
Le difficoltà di lettura globale sono notevoli, anche perché appare arduo riconoscere i punti di inizio e termine di ciascun blocco, nonché la struttura degli annidamenti successivi e le relazioni reciproche.

L'utilità di compressione di Erica trasforma immediatamente la formula così (fig. 13):

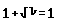
Questo è il livello massimo di compressione e fornisce immediatamente l'informazione che un utente vedente potrebbe afferrare al volo fin dal primo istante: cioè che si tratta della somma di una variabile x più un certo blocco sotto radice, il tutto posto uguale a 1.

Volendo si può esplorare meglio il blocco che qui viene solo abbozzato, passando al livello successivo (fig. 14)

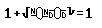
dal quale si può dedurre che dentro al blocco sotto radice c'è una frazione complessa, e così via.

Il software che non c'è
Con queste strategie (marchingegni?) sono riuscito a risolvere alcuni dei più comuni problemi che incontrano gli alunni ciechi con la matematica nelle scuole medie e all'inizio delle superiori, ma complessivamente la questione è ancora ben lontana da essere risolta in modo soddisfacente.
C'è innanzitutto un grosso problema di adattamento delle periferiche braille che per funzionare adeguatamente con le procedure matematiche di Erica devono essere riconfigurate con un codice braille apposito. Si tratta di un'operazione non impossibile ma comunque troppo complessa per essere demandata all'utente finale; il problema andrebbe risolto a monte, definendo e prevedendo una configurazione specifica per tutte le strumentazioni braille destinate alla scuola, o in generale a chi vuole fare matematica in questo modo.
Erica è un prodotto del tutto artigianale; soprattutto in un settore complesso come quello delle strumentazione per ciechi non è sufficiente risolvere un problema qui ed ora, dato che una soluzione efficace in una data postazione può essere del tutto inapplicabile in una diversa.
Tra software e hardware, ovvero tra soluzioni pratiche e strumenti tecnici realmente disponibili, è indispensabile che ci sia una seria interconnessione.
Problemi di adattamento a parte, Erica riesce, almeno per ora, a soddisfare le esigenze degli allievi più giovani, ma per gestire la matematica superiore è necessario un programma più efficiente, simile a TRIANGLE, ma con maggiore attenzione al calcolo e più collegamenti con altri codici e linguaggi: dovrà gestire correttamente anche le stampe, sia in nero che in braille, e disporre procedure di conversione, sia in entrata che in uscita, con altri programmi di scrittura matematica.
Andrà poi affrontato il problema del codice matematico braille per computer a 8 punti. Io non credo che uno stesso sistema di rappresentazione possa andare bene sia per i ragazzini delle medie, che hanno bisogno di un sistema dalla struttura semplice, coerente con il codice standard a sei punti e funzionale soprattutto per esercitazioni in cui il calcolo ha un ruolo fondamentale, che agli studenti dell'università ai quali serve invece un metodo completo ed efficiente per la rappresentazione di concetti e relazioni, il più possibile in grado di interagire con altri metodi di rappresentazione matematica.
Un codice matematico per computer braille a 8 punti adatto per la scuola media e i primi anni delle superiori potrebbe avere queste caratteristiche:
essere il più possibile simile al codice braille standard: in pratica solo il segnanumero verrebbe eliminato, dato che in numeri sarebbero identificati con il punto 6;
conservare i caratteri speciali matematici braille, come quello di inizio e fine numeratore, denominatore ecc. Aggiungere eventualmente il punto 7 o 8 al codice standard per evitare confusioni .;
prevedere una seconda serie di cifre numeriche (da 1 a 0) per i numeratori delle frazioni, con rappresentazione braille abbassata (come per il braille a 6 punti, ma con il punto 8 in più);
tutti i simboli speciali (ovvero usati solo per la rappresentazione braille, senza alcuni corrispondente ordinario in nero) dovranno avere una rappresentazione grafica su video che ne rappresenti in modo evidente e coerente la funzione.
Un secondo codice completo, in grado di rispondere quindi anche ai bisogni della matematica superiore, potrebbe essere progettato in modo da tenere conto di queste esigenze, affinché non si creino spaccature tra una fase e l'altra della carriera scolastica, ma si abbia in pratica un unico sistema, coerente e flessibile, capace di crescere con lo studente adattandosi via via alle nuove esigenze.
L'importante è chiudere definitivamente la fase del "fai da te", dei tentativi ed errori (ma anche dei successi) isolati e poco condivisi, e cominciare ad affrontare seriamente, con i necessari strumenti tecnici e scientifici, i numerosi interrogativi che stanno ponendo l'uso delle nuove tecnologie nella pratica didattica.

Per maggiori informazioni sul software e sui metodi descritti i questa relazione si possono consultare i numerosi documenti, con link alle fonti originali, registrati nel sito Internet:
Provveditorato agli Studi di Vicenza : www.pqs.org/provvvi