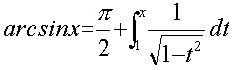GIULIANO ARTICO - Dipartimento di Matematica Pura e Applicata Università di Padova

"Il TeX e i non vedenti"

1. La notazione matematica è bidimensionale
Il linguaggio parlato usuale può essere facilmente fissato in forma scritta perché è costituito da parole pronunciate una di seguito all'altra. Per i concetti matematici non è così: infatti essi prevedono un numero rilevante di costrutti più complessi, che l'esperienza ha portato ad esprimere e codificare in forma scritta con simboli, formule, diagrammi e grafici, tutti strumenti necessari per un uso efficace ed un approccio corretto alla matematica.
É vero che il ragionamento logico-matematico è un'attività astratta che spesso anche i vedenti svolgono mentalmente. Tuttavia il ricorso alla forma scritta è necessario per eseguire i calcoli, per fissare le idee e per comunicare con gli altri.
Chi ha una capacità visiva ridotta o nulla può ricevere le suddette notazioni solo attraverso l'udito e il tatto, dopo che esse sono state adeguatamente adattate. Ad esempio, in un libro di analisi per il liceo possiamo trovare la seguente identità:

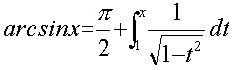
Mentre la formula è semplice da leggere con gli occhi, la sua traslazione in forma parlata è lunga e perde di immediatezza:

"l'arcoseno di x è uguale a pigreco mezzi più l'integrale da 1 a t in dt di 1 fratto la radice quadrata di 1 meno x al quadrato."

Naturalmente la lettura a parole deve essere eseguita dando la dovuta enfasi ai vari elementi, in modo da offrire all'ascoltatore sia la possibilità di comprendere quali sono i simboli coinvolti sia di avvertire le loro reciproche relazioni sintattiche. La mediazione del parlato crea degli ostacoli, pur ammettendo che la lettura sia impeccabile: è facile che, al termine della frase, l'ascoltatore abbia dimenticato l'inizio oppure abbia frainteso un elemento e che quindi si renda necessario ripetere il tutto.
La traduzione della stessa formula in braille presenta difficoltà di natura diversa e non meno problematica: si pensi ad esempio allo spazio che si spreca indicando con uno o più caratteri braille certe proprietà che graficamente si rendono semplicemente sfruttando la disposizione spaziale dei simboli (frazioni, esponenti, eccetera).
In entrambi i casi, le difficoltà della traduzione risalgono sostanzialmente alla necessità di ricondurre ad una forma sequenziale un contenuto che ha marcate caratteristiche bidimensionali.
In matematica, infatti, lo spazio della pagina è sfruttato continuamente con simboli disposti su più livelli (esponenti, pedici, frazioni, matrici) oltre che con diagrammi, grafici e disegni di vario genere.

2. Cos'è il TeX
Il problema della linearizzazione delle formule si presentò a Donald Knuth della Stanford Universitý verso la fine degli anni '70, quando egli si propose di realizzare un sistema di scrittura elettronica capace di trattare le formule matematiche in modo completo e con qualità paragonabile a quella delle migliori edizioni tipografiche: infatti l'informazione doveva essere in qualche modo tradotta in forma sequenziale, perché le memorie del calcolatore sono costituite da elementi posti uno di seguito all'altro.
Il sistema ideato da Knuth si chiama TeX.

Nota 1. La X finale si legge come una C dura perché è la traslitterazione della lettera greca "chi".
Si tratta di un linguaggio basato sull'uso di sequenze di controllo ,dette anche macro istruzioni , ciascuna delle quali è una parola dedicata ad un particolare compito
[4]. Le sequenze di controllo possono essere combinate tra loro per costruire altre sequenze di controllo.

Nota 2. Sono disponibili numerosi insiemi di macroistruzioni, detti package, grazie ai quali il TeX può essere arricchito di caratteristiche aggiuntive.
I package più noti sono LATeX [5, 2] e AMS-TeX [9].

Qui il termine TeX è usato secondo l'accezione più generale e con esso si vuole fare riferimento anche alle sue estensioni.
Una formula matematica si imposta scrivendo varie sequenze di controllo, una di seguito all'altra e con alcune regole sintattiche molto semplici.
Successivamente, durante la fase di compilazione, il TeX costruisce la formula, tenendo conto dei simboli usati e disponendoli nel modo graficamente più idoneo alla visualizzazione e alla stampa.
Il fatto significativo è che la stesura si gestisce benissimo con le periferiche per non vedenti perché, qualunque sia il contenuto, si ha sempre a che fare con ordinari file di testo. Ad esempio, ecco il frammento di sorgente che serve per ottenere la formula riportata più sopra:
$$
\arcsin x = {\pi\over2} + \int_1^x {1 \over \sqrt{1-t^2} } dt
$$
Ogni parola che inizia con \ (barra rovescia) è una sequenza di controllo: \over serve per produrre frazioni, \int rappresenta il segno di integrale, \sqrt quello di radice quadrata, il sottolineato e l'accento circonflesso servono rispettivamente per collocare simboli al pedice e all'esponente, le parentesi graffe delimitano i blocchi di istruzioni, il simbolo $$ serve per iniziare e terminare il modo matematico. Esistono sequenze di controllo per indicare i vari simboli matematici, le lettere greche e molti caratteri particolari.
In questo brano di sorgente non esistono istruzioni di natura tipografica e tutte le relazioni gerarchiche fra gli elementi della formula sono rese usando le specifiche sequenze di controllo e raggruppando certe porzioni di testo fra parentesi graffe. Il TeX stabilisce le caratteristiche estetiche (disposizione e dimensione dei caratteri, spaziature, lunghezza dei segni di frazione, altezza del segno di integrale, eccetera) in modo molto accurato. Esso provvede anche a svolgere tutte le operazioni di formattazione tipiche di un word processor (impaginazione, sillabazione, suddivisione in capitoli, eccetera) in obbedienza ad uno stile che l'utilizzatore può scegliere fra i numerosi disponibili. Tutto ciò è realizzato seguendo le regole stabilite dai tipografi professionisti, regole che l'utilizzatore può ignorare, concentrando invece la sua attenzione sul contenuto e curando il testo dal punto di vista logico.

3. Può un cieco usare il TeX?
Sono un docente cieco che insegna matematica a studenti vedenti. Per svolgere la mia professione ho la necessità di scrivere matematica.
Già da undici anni ho superato la difficoltà grazie al TeX, che uso autonomamente per realizzare materiale a stampa di elevata qualità tipografica (libri di testo, lucidi da proiezione, dispense, articoli scientifici). Recentemente ho anche risolto un problema che sembrerebbe insuperabile per un cieco: quello di produrre autonomamente disegni e grafici (il mio libro di testo [1] contiene oltre duecento disegni, che ho prodotto sfruttando opportunamente le possibilità del TeX).
Così com'è, il TeX non è uno strumento di uso veramente immediato: ciò spiega il basso numero di ciechi che lo adoperano, malgrado esso sia uno standard di fatto nell'ambiente scientifico (ad esempio, quasi tutti i matematici del mondo si scambiano articoli scientifici redatti in TeX e in TeX sono pure disponibili le recensioni su CD-ROM dell'American Mathematical Societý).
Il principale ostacolo è che, mentre un vedente ha la possibilità di leggere il testo nella sua forma grafica usuale, un cieco deve sempre interagire con il sorgente e compiere continuamente una faticosa operazione mentale di filtraggio, al fine di separare l'effettivo contenuto da quelle parole o simboli che costituiscono la parte sintattica del linguaggio.
Lo sforzo non è indifferente per chi scrive il testo e diventa addirittura estenuante durante la lettura di testi redatti da altri, dato che in questo caso il contenuto è sostanzialmente sconosciuto. Chi usa un sintetizzatore vocale non può leggere un sorgente TeX come farebbe con un normale testo perché la concentrazione spesa nell'interpretazione di ciò che si ascolta assorbe gran parte delle risorse intellettuali che sarebbero necessarie per comprendere i concetti contenuti.
Nasce dunque abbastanza spontanea l'esigenza di un'opportuna interfaccia software, orientata soprattutto all'esplorazione delle formule TeX, che permetta ai ciechi di leggerle e gestirle con maggiore facilità.
Una simile interfaccia, qualora fosse realizzata, risponderebbe ad un principio fondamentale, quello che il disabile visivo deve adattarsi il più possibile all'ambiente circostante, popolato normalmente di soggetti vedenti (l'adozione di norme simboliche specifiche per i ciechi avrebbe l'effetto di accentuare il loro isolamento culturale). Infatti il TeX garantisce un aggancio affidabile con la notazione tradizionale, che è frutto di un'esperienza consolidata ed è capace di esprimere esaurientemente e senza ambiguità tutti i concetti necessari. In qualunque modo si proceda, all'utilizzatore deve essere offerta per prima cosa la possibilità di analizzare ciascuna formula e di comprenderne facilmente la struttura.
Nel 1993, nel corso del convegno IWAM di Amsterdam (International Workshop on Access to Mathematics), presentai la mia esperienza e suggerii la realizzazione di un'interfaccia del tipo sopra delineato. Un'idea analoga è stata perseguita negli ultimi anni da alcuni gruppi di ricerca e qui di seguito sono riportati brevi resoconti ed alcuni riferimenti per chi volesse approfondire l'argomento.
Ci sono alcuni risultati interessanti, anche se i software realizzati appaiono allo stato di prototipo o quanto meno in corso di evoluzione.
In generale, la realizzazione di un prodotto software funzionale, stabile e ben collaudato è molto impegnativa, ma lo è tanto più in un progetto di grande complessità, che richiederebbe pertanto risorse ben più sostanziose di quelle impiegate finora verso questa direzione.

4. Il software TeSI
Un prodotto che è liberamente utilizzabile è TeSI, acronimo che sta per TeX to Speech Interface . Questo lavoro è frutto della tesi di laurea di un mio studente, M.Zattera, laureatosi in Ingegneria presso l'Università di Padova nel 1997 [12, 13].
Lo scopo è quello di consentire l'esame delle varie formule contenute in un dato sorgente TeX. Il programma suddivide la formula prescelta in una struttura ad albero, rispettando le relazioni gerarchiche fra i suoi termini, e l'utilizzatore non vedente, mediante una serie di opportuni comandi, può navigare entro questa struttura, ottenendo attraverso la sintesi vocale una descrizione verbale degli elementi man mano incontrati.
La struttura suddetta, detta albero sintattico, non appare in modo diretto all'utilizzatore. Egli riesce a ricostruirne un'immagine mentale attraverso le successive azioni che compie. I comandi sono organizzati in modo da far intuire le relazioni logiche fra gli elementi, e quindi la loro disposizione spaziale, dopo un breve periodo di allenamento. Ecco alcuni comandi:

• frecce orizzontali: fanno scorrere gli operandi di uno stesso operatore, ad esempio gli addendi di una somma oppure il numeratore e il denominatore di una frazione;
• freccia giù: seleziona un operando, passa cioè ad un livello gerarchico inferiore, permettendo così di esplorare più in particolare una porzione della formula;
• freccia su: fa ritornare al livello superiore per esaminare una porzione più ampia della formula;
• Ctrl+frecce verticali: se possibile, selezionano l'esponente o il pedice.

Un particolare importante è che TeSI basa il suo funzionamento su file di configurazione, usuali file ASCII mediante i quali si possono determinare in modo flessibile varie caratteristiche di funzionamento. In particolare, si indicano i comandi TeX che devono essere riconosciuti e si precisa il modo in cui essi vanno letti.
Ad esempio, la seguente istruzione:

• Accento "\overline": "segnato";

dice che \overline x, comando TeX che produce una x con sopra un trattino, deve essere letto "x segnato".
Il programma non si interfaccia direttamente con il sintetizzatore vocale: l'intercettazione del testo da pronunciare è possibile perché le scritte sono prodotte mediante le routine di BIOS del DOS. Ciò costituisce certamente un limite perché impedisce di attribuire al testo quell'intonazione prosodica che aiuterebbe molto l'ascoltatore nella comprensione della formula [6, 10].

Nota 3. Per supplire alla mancanza di intonazione, il programma prevede l'impiego di pause brevi e lunghe, ottenute normalmente mediante segni di punteggiatura.
D'altronde questa scelta favorisce la pressoché totale compatibilità con i sistemi di sintesi vocale esistenti, senza costringere l'utilizzatore all'acquisto di apparecchiature o di programmi specifici.
Sono poi stati adottati accorgimenti per non appesantire l'ascolto: molte informazioni di servizio, come i messaggi di errore e il testo TeX, non passano attraverso il BIOS e non vengono quindi pronunciate dal sintetizzatore. Inoltre la porzione di formula che viene recitata è anche simultaneamente evidenziata nella finestra TeX: ciò può costituire un valido aiuto per un eventuale istruttore vedente.
La limitazione più significativa di TeSI è costituita dal fatto che il programma non è in grado di modificare le formule. Questa funzione può essere svolta solo intervenendo con un editor nel sorgente TeX. Naturalmente sarebbe importante fornire all'utilizzatore la possibilità di eseguire correzioni ed operazioni di taglia e incolla in modo trasparente, con salvataggio automatico in formato TeX.

5. Altre esperienze
ASTER
Anche il software ASTER di T. V. Raman della Cornell Universitý è un programma che accetta come input un testo TeX e produce un'interpretazione parlata delle formule [8, 7]. Questo software sfrutta anche l'intonazione e le pause del parlato per evidenziare come sono raggruppati i simboli. Il programma non è stato reso disponibile, ma ne esiste una dimostrazione su Internet, dove le espressioni matematiche sono fornite in forma grafica, come sorgente TeX e anche sotto forma di file audio.
L'indirizzo è: http://www.cs.cornell.edu/Info/People/raman/aster/aster-toplevel.html.
Per una descrizione del lavoro di Raman si può anche consultare l'articolo [3].

LABRADOOR
La traduzione di sorgenti LATeX in braille è stata invece affrontata da un gruppo dell'Università di Linz (Austria). Questo gruppo ha sviluppato un software chiamato LABRADOOR, termine che significa LaTeX-to-Braille-Door ovvero passaggio da LATeX a Braille.
LABRADOOR è stato sviluppato nell'ambito di un progetto che intende realizzare un ambiente di lavoro matematico destinato ai ciechi e assistito dal calcolatore. Questo software, che è solo un modulo di un più ampio sistema ancora in fase di elaborazione, ha trovato applicazione pratica come programma autonomo per soddisfare le necessità di vari impieghi (ad esempio la produzione di letteratura matematica in braille per studenti della scuola media superiore e dell'università in Austria).
Per maggiori informazioni su questa interessante realizzazione, consultare la pagina Web: http://www.ccr.jussieu.fr/braillenet/ntevh/labradoor.htm.

Bibliografia
[1] Giuliano Artico. Istituzioni di Matematica. Edizioni Libreria Progetto, Padova, 1997.
[2] M. Goossens, F. Mittelbach, and A. Samarin. The LATeX companion. Addison-Wesleý, 1994.
[3] B. Haýes. Speaking of mathematics. American Scientist, 84,2:110-113, March-April 1996.
[4] D. E. Knuth. The TeX book. Addison-Wesleý, Reading, Mass., 1984.
[5] L. Lamport. LATeX: A Document Preparation Sýstem. Addison-Wesleý, Reading, Mass., 1986.
[6] M. H. O'Malley, D. R. Kloker, and B. Dara-Abrams. Recovering parentheses from spoken algebraic expression. IEEE transactions on audio and electroacoustics, AU-21, 3:217-220, 1973.
[7] T. V. Raman. Audio sýstem for technical readings. Ph.d. dissertation, Cornell Universitý, 1994. Audio edition distributed bý Recordings for the Blind, order number FB190.
[8] T. V. Raman. ASTER-towards modalitý-independent electronic documents.
http://www.research.digital.com/CRL/personal/raman/raman.html, 1995.
[9] M. D. Spivak. The joý of TeX: a gourmet guide to týpesetting with the AMS-TeX macro package. American Mathematical Societý, Providence, Rhode Island, 1990.
[10] R. Stevens and A. Edwards. Mathtalk: The design of an interface for reading algebra using speech. In Zagler et al. [11], pages 313-320. ISBN 3-540-48476-5.
[11] W. L. Zagler, G. Busbý, R. Wagner, editors. Proceedings Lecture Notes in Computer Science series - Computer for Handicapped Persons,volume 860, Berlin Heidelberg New York, 1994. Springer-Verlag pubs. ISBN 3-540-48476-5.
[12] M. Zattera. TeSI ausilio informatico per non vedenti per la manipolazione di espressioni matematiche in TeX. Tesi di laurea, Università di Padova, 1997.
[13] M. Zattera. Programma TeSI. Disponibile liberamente alla pagina WEB:
http://www.math.unipd.it/~artico/TeSI.html , Luglio 1997.

Informazioni
GIULIANO ARTICO - Dipartimento di Matematica Pura e Applicata
Via Belzoni 7, 35131 - Padova
E-mail: [email protected]